CF1987G2 Spinning Round (Hard Version)

题目描述

This is the hard version of the problem. The only difference between the two versions are the allowed characters in $s$ . You can make hacks only if both versions of the problem are solved.

You are given a permutation $p$ of length $n$ . You are also given a string $s$ of length $n$ , where each character is either L, R, or ?.

For each $i$ from $1$ to $n$ :

• Define $l_i$ as the largest index $j < i$ such that $p_j > p_i$ . If there is no such index, $l_i := i$ .
• Define $r_i$ as the smallest index $j > i$ such that $p_j > p_i$ . If there is no such index, $r_i := i$ .

Initially, you have an undirected graph with $n$ vertices (numbered from $1$ to $n$ ) and no edges. Then, for each $i$ from $1$ to $n$ , add one edge to the graph:

• If $s_i =$ L, add the edge $(i, l_i)$ to the graph.
• If $s_i =$ R, add the edge $(i, r_i)$ to the graph.
• If $s_i =$ ?, either add the edge $(i, l_i)$ or the edge $(i, r_i)$ to the graph at your choice.

Find the maximum possible diameter over all connected $^{\text{∗}}$ graphs that you can form. Output $-1$ if it is not possible to form any connected graphs.

$^{\text{∗}}$ Let $d(s, t)$ denote the smallest number of edges on any path between $s$ and $t$ .

The diameter of the graph is defined as the maximum value of $d(s, t)$ over all pairs of vertices $s$ and $t$ .

输入格式

Each test contains multiple test cases. The first line of input contains a single integer $t$ ( $1 \le t \le 2 \cdot 10^4$ ) — the number of test cases. The description of the test cases follows.

The first line of each test case contains a single integer $n$ ( $2 \le n \le 4 \cdot 10^5$ ) — the length of the permutation $p$ .

The second line of each test case contains $n$ integers $p_1,p_2,\ldots, p_n$ ( $1 \le p_i \le n$ ) — the elements of $p$ , which are guaranteed to form a permutation.

The third line of each test case contains a string $s$ of length $n$ . It is guaranteed that it consists only of the characters L, R, and ?.

It is guaranteed that the sum of $n$ over all test cases does not exceed $4 \cdot 10^5$ .

输出格式

For each test case, output the maximum possible diameter over all connected graphs that you form, or $-1$ if it is not possible to form any connected graphs.

输入输出样例 1

8
5
2 1 4 3 5
R?RL?
2
1 2
LR
3
3 1 2
L?R
7
5 3 1 6 4 2 7
?R?R?R?
5
5 2 1 3 4
?????
6
6 2 3 4 5 1
?LLRLL
8
1 7 5 6 2 8 4 3
?R??????
12
6 10 7 1 8 5 12 2 11 3 4 9
????????????

3
-1
-1
4
4
3
5
8

说明/提示

In the first test case, there are two connected graphs (the labels are indices):

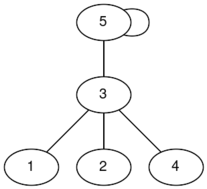
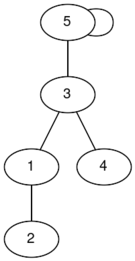The graph on the left has a diameter of $2$ , while the graph on the right has a diameter of $3$ , so the answer is $3$ .

In the second test case, there are no connected graphs, so the answer is $-1$ .